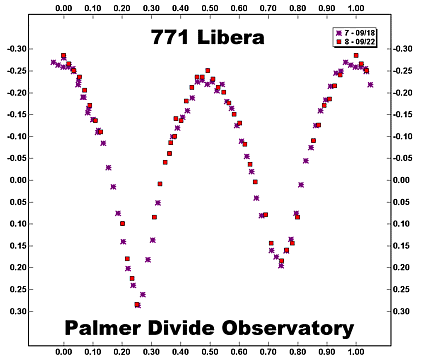
A lightcurve where the amplitude is easy to estimate.
The Fourier analysis routine in MPO Canopus (and other programs) includes an estimate of the amplitude of the curve but it should be used “as-is” with some care. First, if the curve is not completely covered, the analysis attempts to fill in the missing data. This can lead to an amplitude for the curve that is very far removed from the actual value. Also, there might be one or more bad data points, which can affect the amplitude determination.
To be honest, this is where a plot and some common sense come into play. With a
very clean plot, such as the first plot shown below, it is easy to estimate the
maximum and minimum values and assign an amplitude. The amplitude is usually given as the maximum difference in the curve. The curve has two minima, but they
are of different depths. Use the brightest maximum and faintest minimum when making your estimate. In this case, I would give the value as 0.54m ±0.02m.

A lightcurve where the amplitude is easy to estimate.
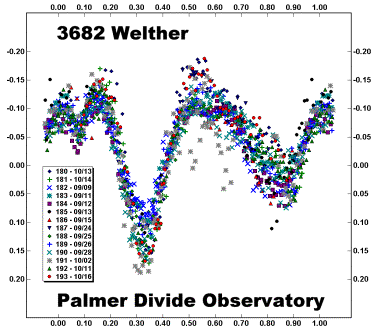
A lightcurve where the amplitude is more difficult to estimate.
The plot in the second figure is not so easy. This is the asteroid I’ve mentioned several times where noisy data was overcome by large amounts of data. This is a great technique for period work but not so good for finding the amplitude. The first rule is do not use the absolute brightest and faintest individual points to find the amplitude. Instead, do a visual estimate of the average value of the maximum. You could also use a spreadsheet, take a range of values near maximum, and have the spreadsheet calculate the mean and standard deviation. Do the same for the faintest minimum. Use the difference between the two values for the amplitude of the curve. If you do use the spreadsheet approach, remember to use the two standard deviations correctly to achieve the final error, i.e.,
Error = sqrt((Error1 * Error1) + (Error2 * Error2))
My estimate for the bottom curve amplitude is 0.28m ±0.03m